Abstract
Low-rank matrix sensing is a fundamental yet challenging nonconvex problem whose optimization landscape typically contains numerous spurious local minima, making it difficult for gradient-based optimizers to converge to the global optimum. Recent work has shown that over-parameterization via tensor lifting can convert such local minima into strict saddle points, an insight that also partially explains why massive scaling can improve generalization and performance in modern machine learning. Motivated by this observation, we propose a Simulated Oracle Direction (SOD) escape mechanism that simulates the landscape and escape direction of the over-parametrized space, without resorting to actually lifting the problem, since that would be computationally intractable. In essence, we designed a mathematical framework to project over-parametrized escape directions onto the original parameter space to guarantee a strict decrease of objective value from existing local minima. To the best of the our knowledge, this represents the first deterministic framework that could escape spurious local minima with guarantee, especially without using random perturbations or heuristic estimates. Numerical experiments demonstrate that our framework reliably escapes local minima and facilitates convergence to global optima, while incurring minimal computational cost when compared to explicit tensor over-parameterization. We believe this framework has non-trivial implications for nonconvex optimization beyond matrix sensing, by showcasing how simulated over-parameterization can be leveraged to tame challenging optimization landscapes.
 style="max-width: 80%; height: auto; display: block; margin: 0 auto;"/>
style="max-width: 80%; height: auto; display: block; margin: 0 auto;"/>
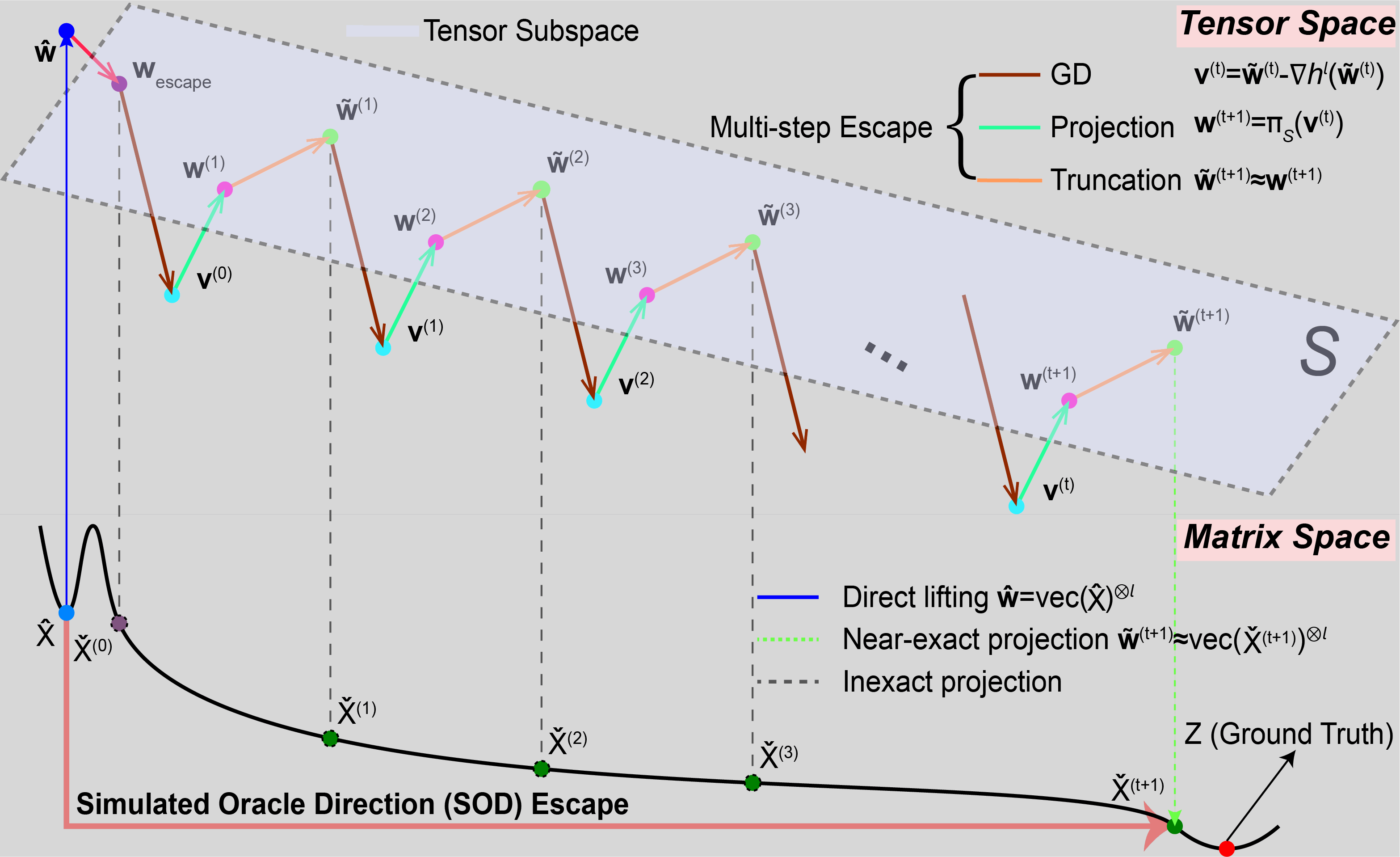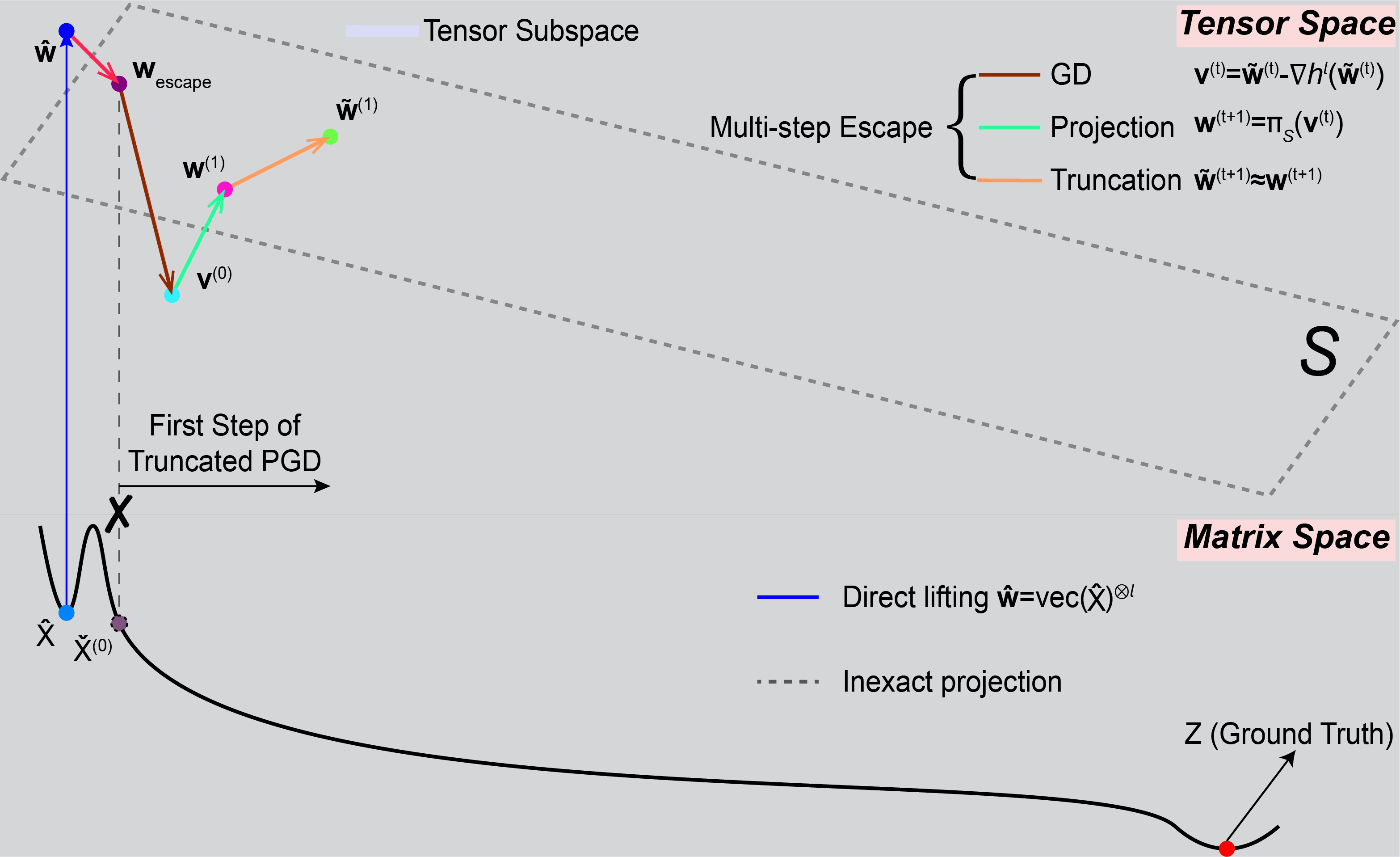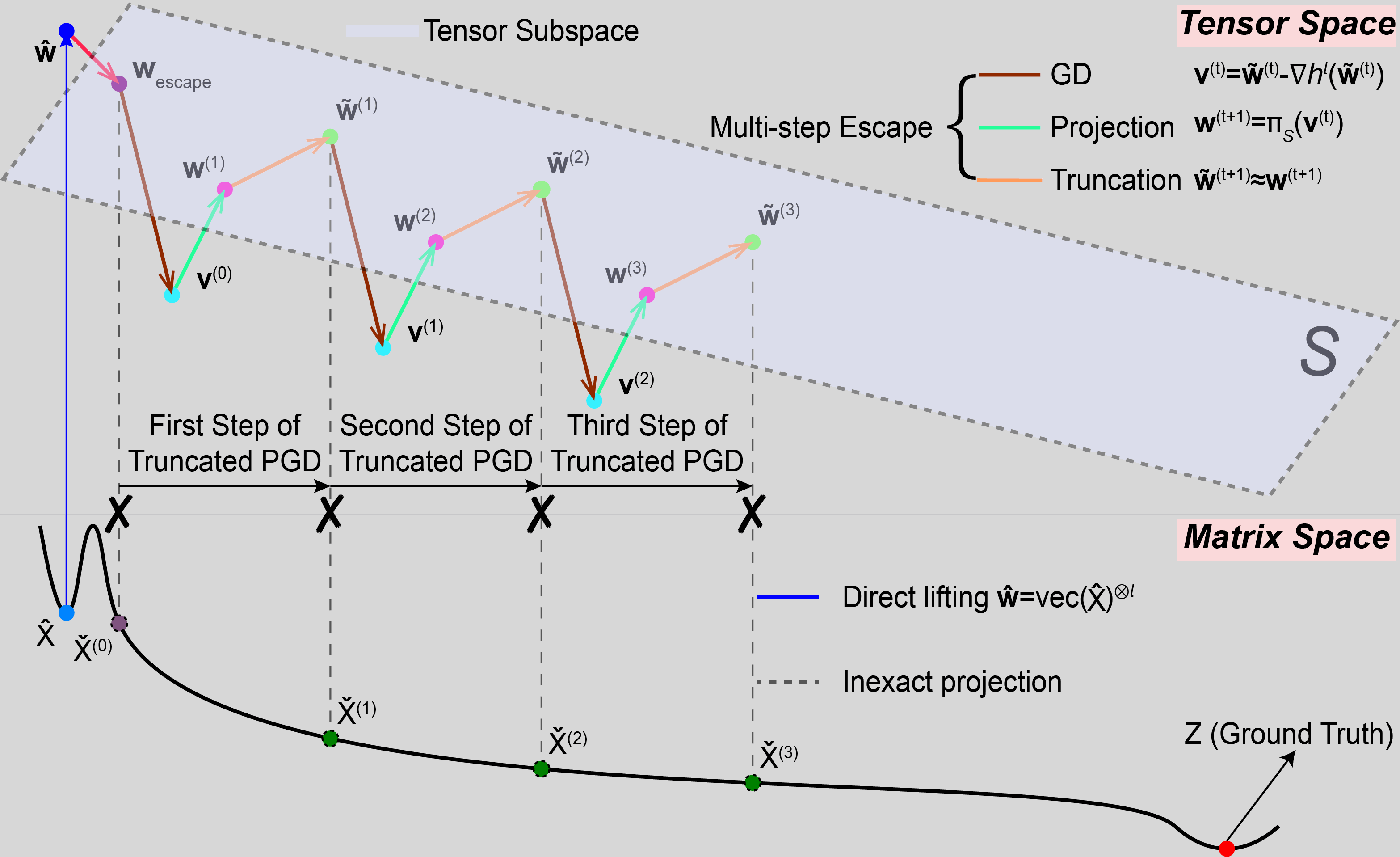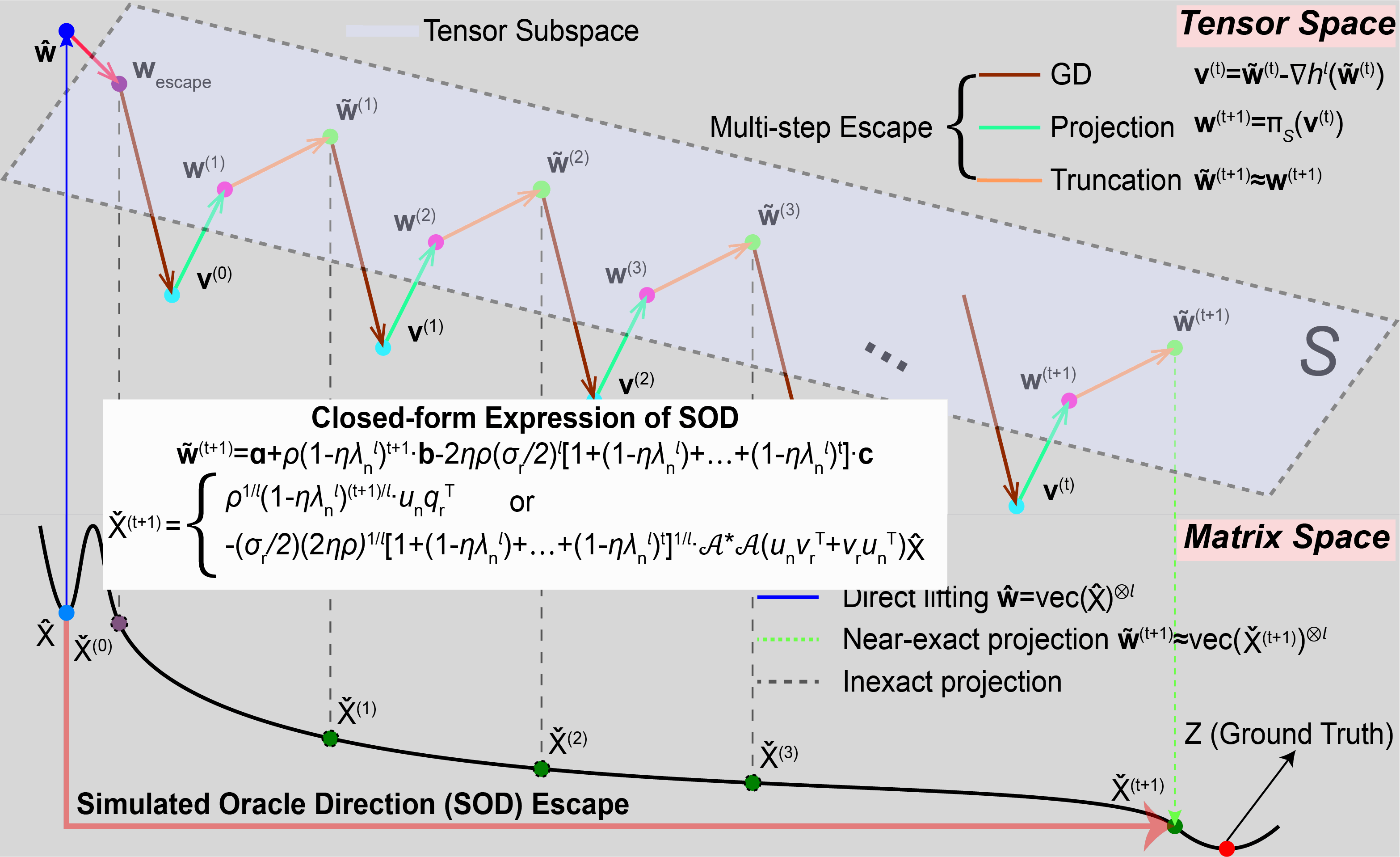
Simulating multi-step tensor-space PGD with truncation after each step, yielding a closed-form iterate X̌(t) that escapes the basin of X̂ along the SOD direction (red transparent arrow).
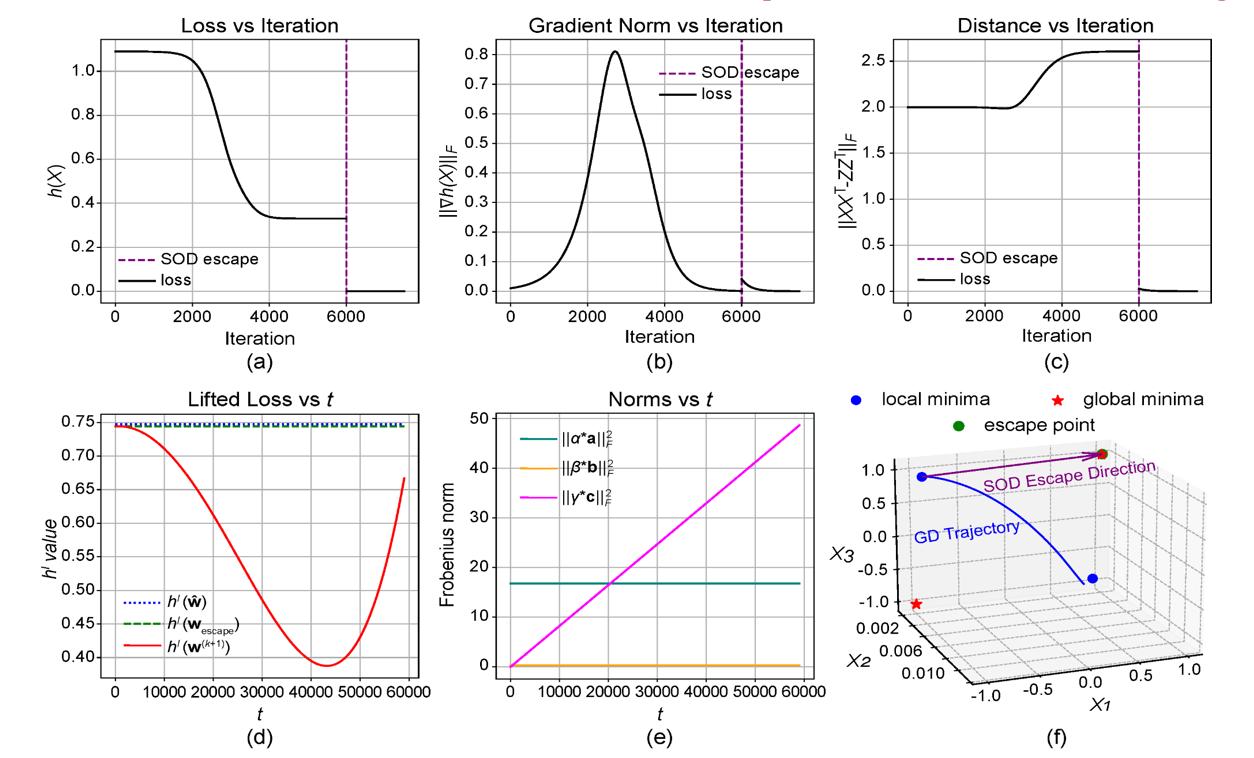
Experimental results of the PMC case. (a) Matrix objective function value vs. iteration. (b) Frobenius norm of the gradient vs. iteration. (c) Distance to ground truth vs. iteration. (d) Tensor objective function value vs. the number of TPGD steps. (e) Frobenius norms of the three tensors within subspace S vs. the number of TPGD steps. (f) Three-dimensional representation of the trajectory of the optimization path.
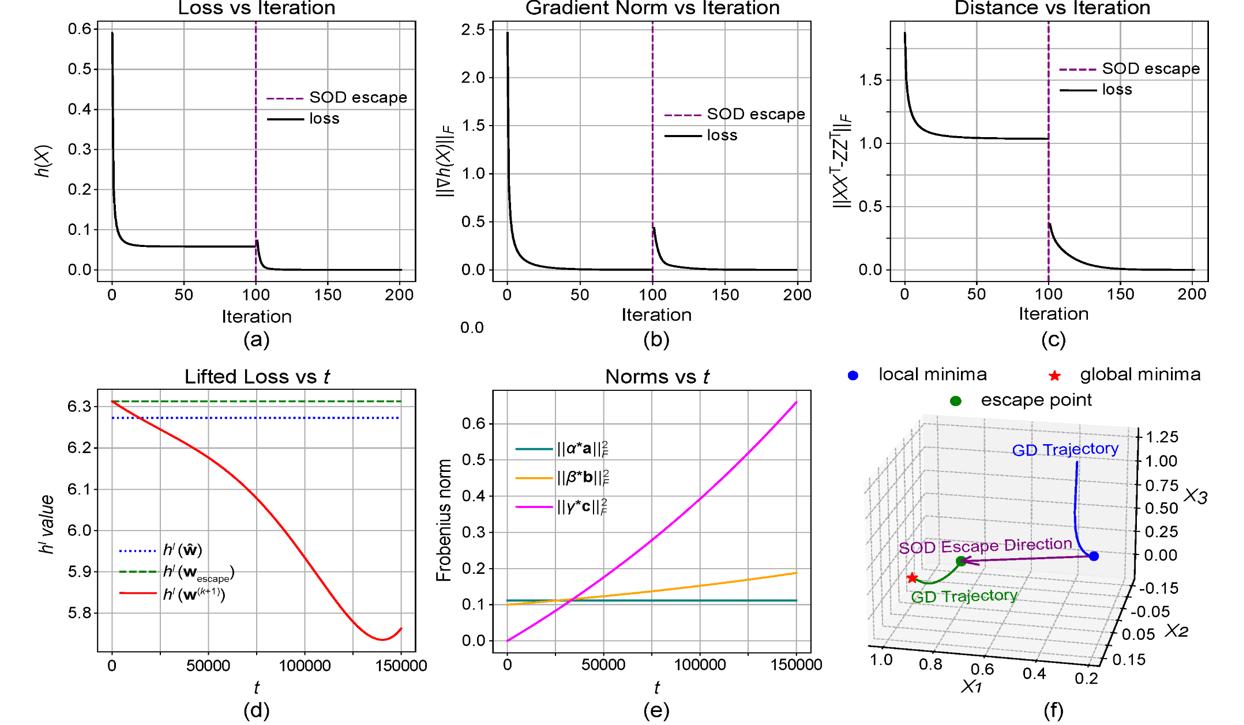
Experimental results of the real-world case. (a) Matrix objective function value vs. iteration. (b) Frobenius norm of the gradient vs. iteration. (c) Distance to ground truth vs. iteration. (d) Tensor objective function value vs. the number of TPGD steps. (e) Frobenius norms of the three tensors within subspace S vs. the number of TPGD steps. (f) Three-dimensional representation of the trajectory of the optimization path.
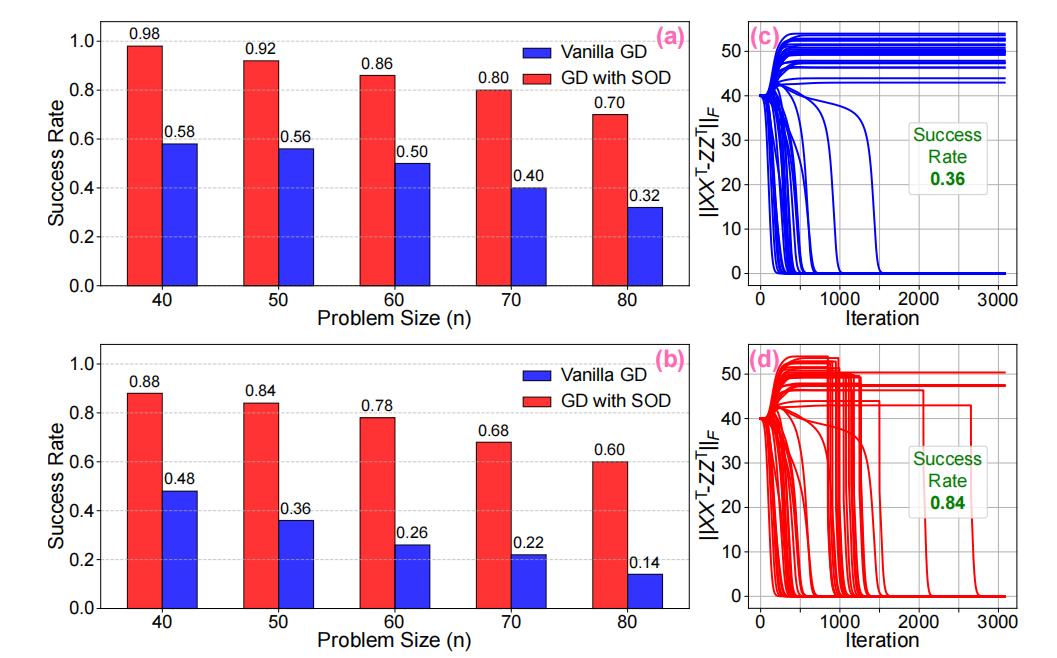
Success rate comparison of vanilla GD and GD with SOD escape.Panels (a) and (b) show the success rates under different problem sizes n, with perturbation parameter ε = 0.15 in (a) and ε = 0.10 in (b). Panels (c) and (d) present the trajectories of ||XXT - ZZT||F over 50 trials across iterations, where (c) corresponds to vanilla GD and (d) corresponds to GD with SOD escape.
Blog Poster
BibTeX
@article{shen2026sod,
title={Escaping Local Minima Provably in Non-convex Matrix Sensing: A Deterministic Framework via Simulated Lifting},
author={Shen,Tianqi and Yang,Jinji and He,Junze and Gao,Kunhan and Ma,Ziye},
journal={arXiv preprint arXiv:2602.05887},
year={2026},
url={https://arxiv.org/abs/2602.05887}
}